Tal i bråkform
Är ett bråktal ett tal, en outförd division, ett förhållande, en kvot eller ett förhållande mellan delen och det hela? Ja, alltihop samtidigt. Bråktal brukar upplevas som svårare än samma tal skrivet i decimalform, trots att de generellt har färre siffror och att de faktiskt betyder samma sak. I det här avsnittet ska vi gå till botten med skillnaderna mellan bråktalens olika skepnader. En av de många användningarna av bråktal är vid procenträkning. Vi använder oss då av delen, det hela och andelen. Andelen utgör både kvoten och procentsatsen, det vill säga förhållandet mellan täljare (delen) och nämnare (det hela).
När ett tal är skrivet i bråkform kan det ses som en division som (ännu) inte är uträknad. Förhållandet mellan täljare och nämnare, kallas kvot. Bråktal är alla tal som skrivs med täljare, nämnare och bråkstreck som till exempel:
$$\frac{3}{4}$$
I ett bråktal står täljaren ovanför (i exemplet 3) och nämnaren (4) under det bråkstreck som skiljer dem åt.
Vi kan dividera bråktalet i exemplet ovan, genom att dela täljaren (3) med nämnaren (4) och få kvoten 0,75. Ibland är det bäst att räkna ut bråkuttryck på detta sätt och ibland är det bättre att låta talet stå kvar i bråkform.
Ett exempel där vi har en sådan situation:
$$\frac{2}{7}+\frac{3}{7}$$
Beräknar vi dessa termer var för sig, får vi ett tal med många decimaler, likaså om vi beräknar summan av de båda decimaltalen. Talet har samma värde i båda formerna om inte decimaltalet avrundats men kan bli otympligt att hantera i decimalform.
Om vi däremot låter bli att beräkna divisionerna och istället tillämpar våra aritmetiska räkneregler kan vi få ett uttryck som har exakt samma värde som det ursprungliga uttrycket och som dessutom är skrivet på en enklare form. Det kan också vara lättare att beskriva ett förhållande om man behåller tal i bråkform.
Låt oss titta på ett exempel på hur vi kan använda bråktal för att uttrycka ett förhållande:
En klass har 12 elever, varav 3 elever använder glasögon. Hur stor andel av eleverna använder glasögon?
Det innebär att andelen elever som bär glasögon är samma som delen av det hela. Med andra ord det antal elever som bär glasögon delat på det totala antalet elever i hela klassen:
$$\frac{3}{12}$$
Tre av tolv elever (tre tolftedelar av alla eleverna) bär alltså glasögon.
Delar av en tårta
Tänk dig att vi har en tårta. Ju fler delar vi delar tårtan i, desto mindre blir varje tårtbit. Delar vi en tårta i tre lika stora bitar och äter en av bitarna har vi tagit \(\frac{1}{3}\) av tårtan. Delar vi istället den ursprungliga tårtan i bara två lika stora bitar och äter en av bitarna så har vi ätit \(\frac{1}{2}\). Då får man en mycket större bit än om vi hade delat den i tre:
\(\frac{1}{3}\)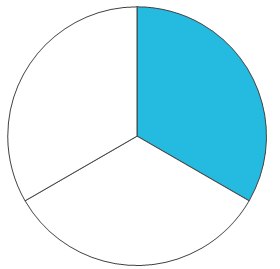 \(\frac{1}{2}\)
\(\frac{1}{2}\)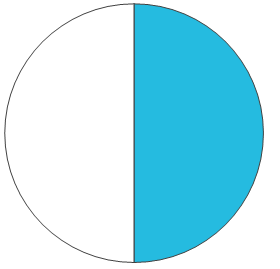
Om man delar en tårta i 12 lika stora bitar och sen äter tre tårtbitar har man på motsvarande sätt tagit \(\frac{3}{12}\) av tårtan. Som vi kan se på bilden nedan är det i själva verket samma sak att säga att man har ätit \(\frac{3}{12}\) av tårtan som att man har ätit \(\frac{1}{4}\) av tårtan - man har ätit lika mycket tårta i båda fallen. Den enda skillnaden är att man i det ena fallet har ätit tre mindre bitar medan man i det andra fallet har ätit en tre gånger så stor bit:
\(\frac{3}{12}\)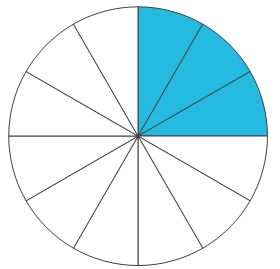 \(\frac{1}{4}\)
\(\frac{1}{4}\)
Man kan beskriva denna likhet så här:
$$\frac{3}{12}=\frac{1}{4}$$
På samma sätt som med tårtan och dess delar fungerar bråk (man kan tänka på det hela som en tårta om man vill). Ju fler delar man delar det hela i desto mindre blir varje enskild del - ju mindre del av det hela varje del är desto större blir nämnaren i bråkuttrycket. Därmed är
$$\frac{1}{3}$$
mindre än
$$\frac{1}{2}$$
En av tre är ju mindre än en av två. I det första fallet har vi ju delat det hela i tre lika stora delar och då blir varje sådan del mindre än om vi bara delat det hela i två lika stora delar.
Det är viktigt att tänka på att bråktal inte bara är tal som är mindre eller lika med ett – som en tårta eller dess delar. Det finns lika många och lika stora bråktal som det finns andra tal – tallinjen har oändligt många bråktal (rationella tal). Ett hjälpfullt sätt att se på bråktal är att betrakta det som ett förhållande mellan täljare och nämnare. De representerar en kvot (utan att man räknar ut kvoten på decimalform) som till exempel delar koncentrerad saft gentemot vatten som ska blandas i ett saftglas.
Här används grafräknaren Casio FX-CG20.
Se samma uppgift med grafräknaren Casio FX-9750GII.
Grafräknare av andra fabrikat har ungefär motsvarande funktionalitet.
- Rationella tal: \(\mathbb{Q}=\{\text{alla tal}\;\frac{a}{b},\;\text{där}\;b\;\text{inte är noll}\}\).
- Förenkla bråktalet
- Lika stora
- Vilket är störst
- Vilket bråktal som har olika värde
- Konvertera till centimeter
- Konvertera till meter
- Addera bråk
- Beräkna talet
- Ett tal mellan två tal
- Hur många av eleverna som inte har ...?
- Vilket som är störst?
- Hitta rätt bråktal
- Räkna med bråktal
- Hitta tal
- Hitta uttryck värde
- Beräkna summan
- Hur mycket koncentrerad saft behöver vi?
