Vinkel mellan räta linjer

Låt oss först försöka rita fallet:

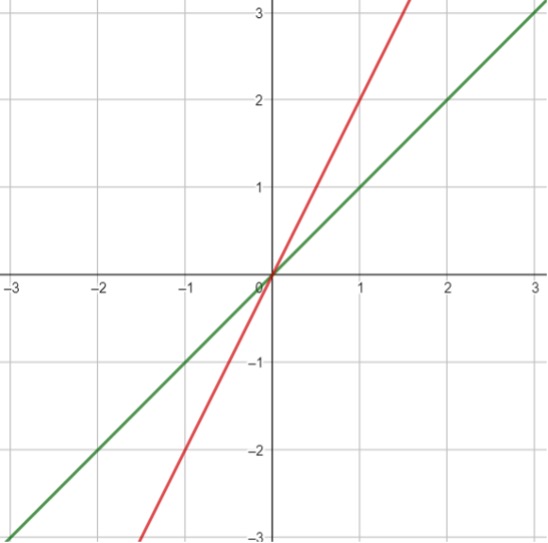
Här söks den spetsiga vinkeln mellan de två linjerna.

Vi kan bilda två rätvinkliga trianglar. Vinkeln som vi söker kommer vara differensen mellan de två vinklarna. Låt oss beräkna de två vinklarna, x och y, var för sig:

Sidornas längder får vi genom att läsa av grafen. Den första triangeln är likbent och detta medför att båda vinklarna är lika med x. Alltså gäller det att:  $$2x+90^\circ=180^\circ$$ $$x=45^\circ$$ Den andra triangelns vinkel fås genom att använda tangens: $$\tan(y)=\frac{2}{1}$$ $$y=\tan^{-1}(2) \approx 63,43^\circ$$ Vinkeln vi söker är skillnaden mellan dessa två vinklar: $$y-x=63,43^\circ-45^\circ$$ $$y-x=18,43^\circ$$

Svar: Den spetsiga vinkeln mellan de räta linjerna \(=18,43^\circ\)