Kvantitativa jämförelser
13. \( \frac{8}{10} = \frac{x}{16} \)
- Kvantitet I: x
- Kvantitet II: 10
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Multiplicera båda led med 16:
\[ \begin{align*} 8 \cdot 16 / 10 &= x \\
128 / 10 &= x \\
12,8 &= x\\
x &> 10 \end{align*} \]
Svar: A
14. Almas ålder är hälften av Ellas och Lenas sammanlagda ålder.
- Kvantitet I: Almas ålder
- Kvantitet II: Ellas ålder
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Man kan tänka på olika exempel där A, B eller C håller.
A: Alma = 5 år, Ella = 3 år, då kan Lena vara 7 år gammal för att Almas ålder skall vara hälften av Ellas och Lenas sammanlagda ålder
B: Alma = 5 år, Ella = 7 år, då kan Lena vara 3 år gammal
C: Alma = 5 år, Ella = 5 år, då kan Lena vara 5 år gammal
Därför behöver vi mer information för att kunna bestämma ett förhållande mellan Almas och Ellas ålder.
Svar: D
15.
- Kvantitet I: 30 procent av 40
- Kvantitet II: 40 procent av 30
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Lösningsförslag:
Kvantitet I: \( 30 \% \text{ av } 40 = 30 \cdot 40 / 100 = 12 \)
Kvantitet II: \( 40 \% \text{ av } 30 = 40 \cdot 30 / 100 = 12 \)
Svar: C
16.
- Kvantitet I: Medelvärdet av mätserien 1, 3, 7
- Kvantitet II: Medelvärdet av mätserien 1, 1, 3, 7, 7
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Lösningsförslag:
Kvantitet I = \( \frac{1 + 3 + 7}{3} = \frac{11 }{3} \)
Kvantitet II = \( \frac{1 + 1 + 3 + 7 + 7}{5} = \frac{19}{5} \)
Förlänga för att få samma nämnare:
Kvantitet I: \( \frac{5 \cdot 11 }{ 5 \cdot 3} = \frac{55}{ 15}\)
Kvantitet II: \( \frac{ 3 \cdot 19}{ 3 \cdot 5} = \frac{57}{ 15} \)
Svar: B
17. Linjerna \(L_1\) och \(L_2\) är parallella
- Kvantitet I: x+ y +z
- Kvantitet II: \(180^\circ \)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
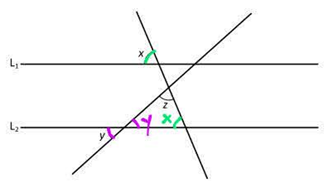
I den större triangeln som skapas mellan linjerna med vinkeln z har vi en vinkel som är vertikalvinkel med y och en som är likbelägen med x. Summan på en triangelns vinklar är alltid 180 grader, därför är summan av x, y och z också 180 grader.
Svar: C
18. \( x \neq 0 \)
\( x^2 = -5x \)
- Kvantitet I: x
- Kvantitet II: 0
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Andragradsekvationen ger två lösningar. Ett där x=0 och ett där x=-5. Men enligt uppgiften fick x inte vara lika med 0. Alltså är x=-5. II är då större än I. (0 är större än -5)
Svar: B
19. Arean av en rektangel är 50 cm2. Rektangelns bredd är 5
- Kvantitet I: Längden av rektangelns diagonal
- Kvantitet II: 11 cm
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Längden på rektangeln måste vara 10. Då kan man med hjälp av Pythagoras sats räkna ut att diagonalen är roten ur 125. 11 i kvadrat är ju 121. Alltså är diagonalen längre.
Svar: A
20.
- Kvantitet I: \( \frac{3^2}{7^2} \)
- Kvantitet II: \( \frac{7^{-2}}{3^{-2}} \)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Ett tal med en negativ exponent byter tecken på exponenten om den flyttas täljare till nämnare eller tvärtom. Det betyder att Kvantitet II kommer att bli exakt lika som kvantitet I.
Svar: C
21. Linjen L går genom punkten (-10, -1) och har positiv lutning
- Kvantitet I: y-koordinaten för den punkt där L skär y-axeln
- Kvantitet II: 0
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Vi vet inte vilken lutning linjen har, därför kan vi inte veta var på y-axeln linjen skär.
Svar: D
22. \( y \neq 0 \)
\( \frac{2x}{3y} = 7 \)
- Kvantitet I: y
- Kvantitet II: \( \frac{2}{21}x \)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Vi bryter ut y ur ekvationen.
$$\frac{2x}{3y}\cdot 3y = 7 \cdot 3y$$
$$2x = 21y$$
$$y=\frac{2x}{21}$$
Vilket är detsamma som Kvantitet II.
Svar: C